1)이변량 상관계수는 두 변수간에 상관관계(선형성)를 보는 분석방법입니다.(두변수 모두 구간형 척도일때 활용합니다) 예를들어 키와몸무게의 상관관계(두자료 모두 구간형이죠?), 광고액과 매출액의 상관관계(이것도 구간형)등이요
2)회귀분석의 경우 앞서 말한 상관분석 결과 유의한 결과를 얻었다면(예를들어 광고액이 높으면 매출액도 높더라) 그중 독립변수라고 생각되는 것이 종속변수를 얼마나 설명할까를 수식으로 표현한 것입니다.
물론 기본적으로 종속변수가 구간형 자료일때 사용가능합니다. 하지만 로지스틱 회귀분석이라고
종속변수가 범주형일때 사용가능한 회귀분석도 있습니다
3)교차분석 자료가 아래 표와같이 범주형자료로서 교차표를 작성 가능할때 사용합니다.
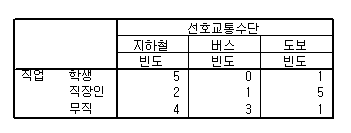
위자료는 제가 방금 조작해서 만든거고요, 교차분석의 경우 직업과 선호교통수단이 어떤 연관관계가
있을까 하는 궁금증이 들때 사용합니다.
4)일표본T검정의 경우 한 변수의 모평균을 검정해 내는 것입니다.
예를들어 제가 고등학생 100명의 키를 가지고 있다면 이자료를 가지고 모집단(우리나라 전체 고등학생)의
키를 검정해보는 자료입니다. 물론 모든 T검정은 종속변수가 구간형일때 가능합니다.
5)독립표본T검정의 경우 일표본과는 달리 다 집단간의 평균차이가 존재하는지 검정합니다.
예를들어 남자,여자간에 키의 차이가 다를까? 학생과 직장인 사이에 토익점수에 차이가 있을까? 등등요
6)대응표본T검정의 경우 독립T검정처럼 두 집단간의 평균차이가 존재하는지 검정하는 것이지만,
종속적인 집단간의 비교라는 점이 다릅니다. 예를들어
학원다니기 전 1반 학생들의 영어 점수 VS 학원다닌 후 1반 학생들의 영어 점수
똑같은 사람인데 어떤 교육 전과 후 등의 차이를 검정할때 사용합니다. 독립은 남/여 등 아예 다른 집단이었죠?
7)일원배치분산분석은 독립T테스트의 연장선이라고 이해하시면 됩니다. 독립T테스트가 두 집단간의 평균차이를검정했다면 일원배치 분산분석의 경우 세개 이상집단의 평균차이를 검정할 때 사용합니다.
예를들어 미국인,한국인,일본인들의 키 차이.
8)카이제곱 검정은 동질성 검정과 독립성 검정 두가지로 나눠집니다. 독립성검정은 앞서 말씀드린 교차분석때
실시하는 것이고요, 동질성의 경우 비율이 같은지 검정하는 것입니다. 예를들어 우리나라가 이번 올림픽때
메달을 땄는데, 금,은,동 메달의 비율이 같을까?를 알아볼때 사용합니다~~
9)일표본 K-S검정은 분포모양을 알아볼때 사용합니다(별로 안쓰실 꺼에요)-구간형일때
10)독립2-표본비모수 검정 = 독립T검정의 비모수적 검정법
독립2-표본비모수 검정은 독립T검정과 같은 목적일때 사용하고요, 이걸 쓰는 이유는 모집단의 분포를
모르거나 정규분포가 아닐때, 또는 가지고있는 자료의 숫자가 너무 적을때 사용합니다. 일반적으로
중심극한정리에 의해 자료의 개수가 30이상이면 정규분포를 따르므로 30개 이하일때 이 검정을 사용하시면
됩니다.
11)독립K-표본 비모수 검정=일원배치분산분석(사용이유는 위와 동일)
12)대응 2-표본 비모수 검정=대응T테스트(사용이유는 위와 동일)

